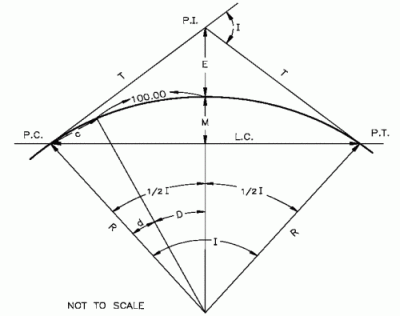
HORIZONTAL CURVE FORMULAS
| D | = Degree of Curve,
Arc Definition
| | 1° | = 1 Degree of Curve
| | 2° | = 2 Degrees of Curve
| | P.C. | = Point of Curve
| | P.T. | = Point of Tangent
| | P.I. | = Point of Intersection
| | I | = Intersection Angle;
Angle between two
tangents
| | L | = Length of Curve,
from P.C. to P.T.
| | T | = Tangent Distance
| | E | = External Distance
| | R | = Radius
| | L.C. | = Length of Long Chord
| | M | = Length of Middle Ordinate
| | c | = Length of Sub-Chord
| | k | = Length of Arc for Sub-Chord
| | d | = Angle of Sub-Chord
|
|
|
| R = | L.C. | | T = R tan(I/2) = | L.C.
|
|
| | 2 sin(I/2) | 2 cos(I/2)
|
| L.C. | = R sin (I/2) | | D1° = R = 5,729.58 | | D2° = | 5,729.58 | | D = | 5,729.58
|
|
|
| | 2 | 2 | R
|
M = R [1 - cos(I/2)] = R - R cos(I/2)
| E + R | = sec(I/2) | | R - M | = cos(I/2)
|
|
| | R | R
|
| c = 2R sin(d/2) | | d = | kD
|
| | 100
|
| L.C. = 2R sin(I/2) | | E = R [sec(I/2) - 1] = R sec(I/2) - R
|
| ![]()
